Bullet Drop

Bullet Drop:
How Do You Calculate It? Does It Matter for Pistol Shooters?

 

Welcome back, readers! Today we’re going to talk about a topic that long range rifle shooters deal with, and generally know how to handle but pistol-only shooters may find it a bit confusing: bullet drop. How far does the bullet drop due to gravity when it leaves the barrel of your gun? How can you calculate that? How does that affect where rounds will impact?

First, all bullets are affected by gravity, and will fall to earth at the same acceleration rate, regardless of their weight or size (we’re making a small simplification here, neglecting air resistance, but the difference is small compared to the effects of gravity at short ranges, so we’ll ignore air resistance). This (perhaps surprising) result was discovered over 400 years ago by the legendary scientist Galileo, when he dropped objects of different weights off the leaning tower of Pisa and they hit the ground at the same time! (Figure 1)

Of course, if a bullet is fired in an upward direction, it will travel some distance upward (depending on the angle and on the bullet’s speed), but from the moment it leaves the barrel, it is being pulled downward by gravity. If gravity was not affecting the flight, then anytime an object were to be fired upward, it would simply keep going in a straight line in the direction of the bore axis, but we know that’s not the case (Figure 2).

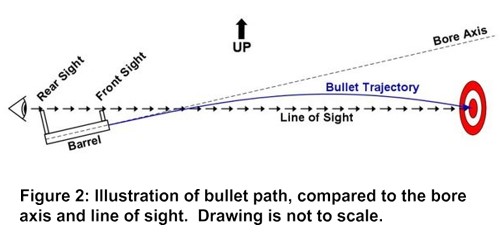That upward launch angle can be accounted for, but a simpler case to analyze is when there is initially horizontal flight. If a bullet is fired horizontally (no upward angle), and another bullet is dropped at exactly the same time from the same height, they will both hit the ground at exactly the same time! Gravity is pulling on both at exactly the same rate, regardless of the initial launch angle, but the case where it’s fired horizontally is easier to understand and calculate.

So how do we calculate how much the bullet will drop before it hits the target? To do this calculation accurately, the math gets a little bit complex…unless we make a couple of simplifying assumptions. The trick, then, is to evaluate whether those assumptions are close enough to the real situation so that they are valid. What are those assumptions?

First (as previously discussed), we’re going to assume that the round is fired in a more or less horizontal direction. This is generally the case when pistol shooting; most times, the target is within a small angle of horizontal from the barrel. If you are shooting uphill or downhill at a big angle, the math changes; mathematically, you’d have to add in a cosine of the shooting angle times the initial velocity, but we want to keep things simple here, so we’ll assume we’re shooting approximately horizontal, and neglect that factor.

The next simplifying assumption is that we’re going to neglect air resistance (‘wind drag’). For long range shooting, you clearly CANNOT neglect air resistance; this is a factor that long range shooters must account for… but at short ranges (let’s say, under 100 meters) it’s really not going to matter much, so for pistol shooters (and long gun shooters at very short ranges), we can safely neglect air resistance.

With those simplifications, the bullet drop equation simplifies down to just one variable: time of flight. Since we made the assumption that we’re going to ignore wind resistance, we can use the muzzle velocity of the round to calculate time of flight. For longer ranges, this is where things get tricky, because the bullet is slowing down more and more, the farther it goes, due to that air resistance. Calculating that properly is a bit more complicated; however, at the shorter range we’re considering, we can just use the muzzle velocity and keep it simple.

Muzzle velocity has units of (in English units) feet per second, so if we know how far away our target is, we just divide that distance by the muzzle velocity, and we get the number of seconds (it’s going to be a fraction of a second at short distances) that the bullet flies before it hits the target. When doing this, remember to be careful to stay within the same units of measurement; if you are working in English units, it will be feet. If the muzzle velocity were given in metric units, it would be in meters. Most of the time, the muzzle velocity will be printed on the ammo box; in the US, the units are generally English units. Even the listed muzzle velocity carries some assumptions (the muzzle velocity was measured by firing the round out of a barrel of a certain length) but for our purposes, it’s close enough. Here’s that time of flight equation:

T = (target distance) / (muzzle velocity)

Now that you know the time of flight of the bullet to the target (with all of our assumptions), we can easily calculate the bullet drop, using this equation:

D =  ½ g t²

In this equation, D is the drop distance that we are calculating, t is the time of flight (which we previously discussed) and g is the gravitational acceleration. In English units, g is equal to 32.17 ft/sec². If you are using Metric units, that constant is 9.81 meters/sec².

As an example, let’s consider a 9mm round that has a muzzle velocity of 1100 ft/sec. This can vary with different makers of ammunition, but that’s within the typical range. If you are shooting at a target that is 30 feet away, then the time of flight is:

T = (30 feet) / (1100 feet/sec) = 0.0273 seconds

As you’d expect, the bullet gets to the target (at this short range) faster than the blink of an eye! So how far did it drop during that time?

D = ½ (32.17 ft/sec²) x (0.0273 sec)² = 0.0120 ft

Converting 0.0120 ft into inches, we see that the bullet drop (in this case) is about 0.144 inches… so the bullet dropped a hair over ⅛ inch at that range!

If we went through the same math with a slower bullet, such as 0.45ACP (we’ll assume a muzzle velocity of about 850 feet/sec for that), you’d find that the bullet drop for that is almost a quarter inch at 30 feet (0.24”). Clearly, the slower the bullet, the more it drops. This makes sense; bullets that fly really fast don’t have enough time to fall as far as slower flying bullets.

One thing to note is that due to the time factor being squared, doubling the distance does not just double the amount of drop. I’ve gone ahead and calculated the approximate bullet drop for different calibers (average muzzle velocities) at different ranges, this is shown in Table 1.

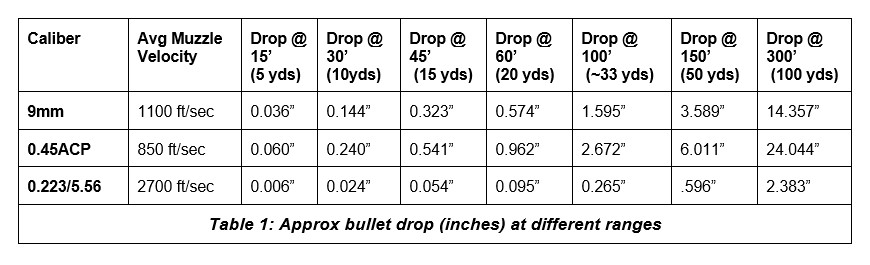Those results may surprise some people. While the bullet drop for an average 9mm round at 20 yards (60 ft) is only a little over half an inch, if you take it out to 50 yards, the bullet drops over 3.5 inches… and if you double that and go to 100 yards, it drops more than 14.3”! The effect of bullet speed in both directions is seen by the other entries in this table; a slow 0.45ACP round will drop over 24” at 100 yards, while the speedy 5.56mm round will only drop about 2.4” in that same 100 yards. Also, we are slightly under-predicting the amount of drop, due to our simplification of neglecting air resistance…but this calculation gets you in the ballpark.

So how much does bullet drop matter? Well, that depends a lot on what caliber you are using, and the range you are using it at. Most handgun shooting is done at ranges of about 20 yards or less (often, much less), so for most pistol shooters, if you sight in at the mid-point of that range (about 10 yards), you’re going to be within about plus or minus a quarter inch (maybe less) of your point of aim, all the way from point blank range out to about 60 feet. If you happen to find yourself shooting a pistol at longer ranges (unusual, but it could happen) then you may have to account for a bit more bullet drop.

Figuring out how much a bullet drops really isn’t hard, you just need to know the muzzle velocity and the distance to your target. With that info, and a couple of assumptions, you can get a good estimate of how far it will drop.

We hope you enjoyed this article. We try to pick a range of topics, including historical events & guns, practical carry considerations, and a few somewhat technical topics. If you’ve missed any of the articles, you can find them posted on our website: www.selectfiretrainingcenter.com/posts.

We hope to see you at the range, come out and train with us!

 

 

Like this article? Please consider sharing and leave your comments below!

Select Fire Training Center (SFTC) is the premiere training center and indoor shooting range facility in Northeast Ohio. Dedicated to offering a top-notch facility with highly skilled instructors, a wide range of classes and a state-of-the-art shooting range experience. We are here to serve your needs, make you feel welcome and we do this by offering you true customer service by friendly, knowledge people.